
The humble d20 hails back to Roman times, but is most famous for its prominent role (!) in the Dungeons and Dragons role-playing game. D&D is also renowned (amongst those familiar with it) for using a variety of different dice-systems throughout.
3d6 for Character Creation. 1d6 for Searching. Percentile dice for Thieves Skills, 2d6 for Clerical Turning of Undead, the list goes on.
Other games have tried (with varying degrees of success) to limit the types of rolls that are made. Apocalypse World (and its descendants) use 2d6 exclusively. Rolemaster uses Percentile dice for everything.
But what difference do the different types of rolls make?
Swings and Spikes
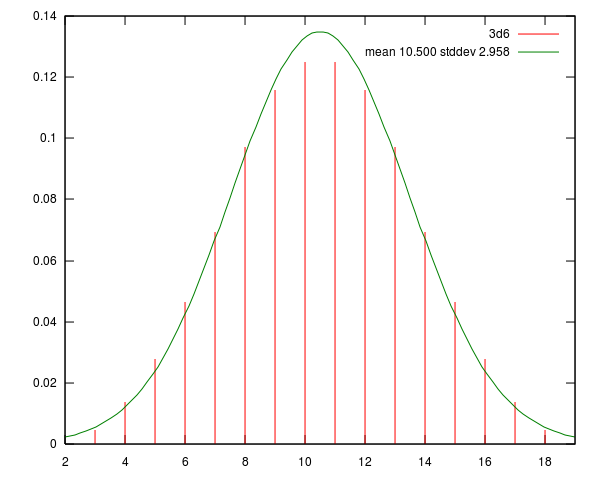
A term often heard when discussing dice systems is “Swingy”. Usually used in relation to 1d20 or percentile rolls, it means that the result can vary hugely, on a flat probability scale. It “swings” from one end to the other randomly.
“Spikey” rolls, on the other hand, are highly biased towards particular results, such as the bell-curve of 3d6.
While both 1d20 and 3d6 give very similar average results, the change of getting any result varies hugely.
in our current game, we decided that the 1d20 roll that the system uses was too “swingy”, and have replaced it with 2d10. This should give a more reliably-average roll, without taking Luck entirely out of the equation.
How do you Roll?
There are a few Major systems for determining the result of a dice roll:
- Dice+Bonus: e.g. D&D 5e (1d20+Stat Modifier+Proficiency), Rolemaster (1d100+Skill Bonus).
- Roll under Skill: e.g. GURPS (3d6), Runequest (1d100).
- Dice Pools: Roll multiple Dice. each one that beats the target Number counts as a Success. Beat a “Number of Successes” to succeed. e.g. White Wolf (Vampire et al)(1d10 per “dot” of skill, looking for 7s).
(These are by no means the only systems, but do represent the most used.)
It is relatively easy to calculate the Average roll using these systems.
3d6 -> 10.5, d100 -> 50.5, 1d20 -> 10.5 etc.*

*White Wolf dice pools vary hugely across editions. I shall be referencing Exalted 3e, which calls for targets of 7, with a roll of “10” counting as 2 Successes. This gives an average roll of half the number of dice rolled. 6 dice -> 3 Successes. 10 dice -> 5 Successes.
We can quickly figure whether an Average result is enough to succeed:
e.g. Bob the Fighter rolls 1d20 +5, needing a 15. That’s a pretty close call (15.5 average)
Ann the Animist rolls 1d100 +30, needing a 100. Unlikely, but possible.
Carol the Caroller rolls 8d10 needing 3 Successes. Almost certain, one might think …
Far From the Average Roll
While some systems are famous (justly or unjustly) for their complexity and requirements of Advanced Mathematical Knowledge (I’m looking at you, Rolemaster!), while others are so simple it hurts, it is always useful to have a bit of a grasp on what the numbers mean.
Average Rolls are a good start, but what if you need a non-average roll?
1d20 vs 15+ is easy enough. 30% chance, about 1 in 3. (Each “pip” of a d20 is 5%. 15, 16, 17, 18 19, 20 = 6 options. 6*5% = 30%)
3d6 vs 14-? Likely, but how likely? This graph (Courtesy of AnyDice.com) shows that it is 90% likely!

The “Spikiness” of 3d6 means that if the required roll is better than 50/50, it soon becomes very favourable.
Carol (above) needs 3 successes from 8 dice … a more complex situation. We know that it is better than 50/50 (as that would be 4 successes). Thankfully, Scott Gray has created a Dice Pool Calculator to do the heavy-lifting for us! His calculations show that 3+ is a 68.5% chance. About 2 in 3.
Custom Modifications
Now we have an idea of the basic rolls, what about when they change? Is the darkness giving us a 2 point penalty on our Observation? Does our Long Stride give us a 2 point bonus on Chases? How much difference does this make?
On a “flat” dice, such as 1d20 (or almost any “single dice” system), a set modifier gives a set change to our chances. On 1d20, every shift is equal to a 5% change. +2 is +10%. -3 is -15%.
On 3d6, it depends where on the curve you are! The difference between 6- and 9- (a 3 point bonus) is the difference between 9% (say 1 in 10) and 37% (say 1 in 3, or 3 in 10). That’s +30%!
But 3d6 needing 12-, with a 3 point bonus (so 15-) only shifts from 74% to 95% (+20%)!
With a “spiky” roll, it makes a big difference whether you can get enough Bonuses to move the “spike” across the required roll!
Once more, for the hard-of-rolling:
Some systems have a way of re-rolling a result (or part of it).
Exalted 3 has several Charms that allow you to take dice of a certain value and roll them again (e.g. Excellent Strike: “Attacks gain one automatic success, and 1s are rerolled until they no longer appear“).
D&D 5 has included “Advantage” (Roll 2 dice and take the better roll) and “Disadvantage (Roll twice and take the worse roll)
A method I have seen, but don’t recall where from, is a way of changing a “swingy” roll into a “spikey” one. Instead of rolling 1 die, you roll 3, and take the middle one! This moves the expected result strongly towards the middle of the range, and makes the extreme rolls very rare indeed! (To roll a “1” on 3d20-middle requires all 3 dice to turn up “1”, a 0.0125 percent chance, rather than a 5%!
Sorry, you lost me …
Don’t worry! The only thing you really need to know is which dice to roll, and what number you need. Knowing the average, and therefore roughly how likely you are to succeed is useful, and quickly learned.
If you are interested in the probabilities, and the shapes of particular curves, anydice.com has some very useful tools.
Summary
There are many different rolling methods, but so long as you can get to grips with the one that is used in your game, you are set!
Always keep a supply of several dice-types, in case they are needed, and don’t be afraid to switch out poor dice!
